The velocity gradient tensor in turbulence
WEDC Staff involved: Chris Keylock
Summary of project activities
The Navier-Stokes equations govern the behaviour of the flow of air and water. It is often useful to take the spatial derivative of these equations to obtain the velocity gradient tensor (VGT). This has the nice property that it incorporates the incompressibility condition.
Classically, the VGT is then studied in terms of the strain rate and rotation rate components or its eigenvalues, or invariants. For example, flow structures in a turbulent flow over bedforms are visualised in the figure below using the second invariant of the VGT. We have developed an alternative approach to the analysis of the VGT. So far, we have been working on the implications for idealised cases, with a view of moving towards more application-based research.
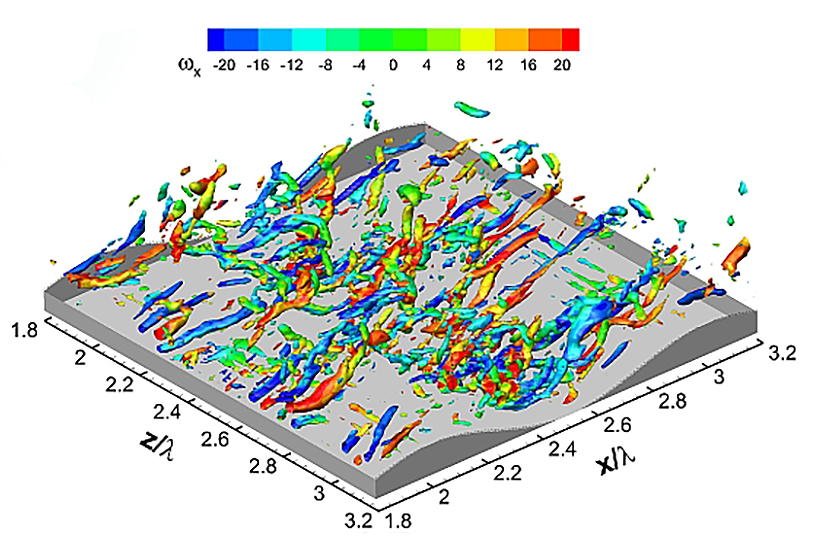
Above: An examination of one component of the vorticity field within coherent flow structures for a turbulent flow over bed-forms. The coherent structures are extracted using the second invariant of the velocity gradient tensor.
Summary of project outcomes and impact
We have a number of potentially important results so far:
- At small scales (of the order of the Kolmogorov scale), the contribution of the non-normal component to the dynamics is of similar magnitude to the normal (eigenvalue-related part).
- We have clarified why it is that the vorticity tends to align with the intermediate eigenvector of the strain rate tensor, and have used our approach to explain why turbulence tends to form disc-like, rather than rod-like flow structures.
