Mathematical Sciences
Qualification(s) available: PhD
- Entry requirements
- 2:1+
- Fees for 2024-25 (per academic year)
-
(Self-funded)UK: £4,786International: £21,500
- Fees for 2025-26 (per academic year)
-
(Self-funded)UK: £5,006International: £22,360
- Fees
-
(Self-funded)Dependent on start date. See below.
- Full-time
- 3 years
- Part-time
- 6 years
- Start date
- 1 January, 1 April, 1 July or 1 October
- Location
- Loughborough
- Subject area(s)
- Mathematical Sciences
Overview
Our Mathematical Sciences department is committed to driving forward innovation in both pure and applied mathematics.
We attract staff and students from all over the world, making our department a diverse and stimulating environment in which to study. Active in high-quality research across the broad spectrum of mathematics, we have an excellent international reputation.
Our PhD programme will allow you to delve deeper into a topic you are passionate about and make new discoveries, with our excellent state-of-the-art laboratories and facilities providing a platform for world-class research. The knowledge, skills and expertise gained can be transferred into a career in mathematics, research or academia.
Our key research themes include analysis, dynamical systems, geometry and mathematical physics, linear and nonlinear waves, mathematical modelling, statistics, and stochastic analysis. We also host regular seminar series and colloquia, as well as international conferences and workshops.
As part of the School of Science, our Mathematical Sciences staff and PhD students contribute to our interdisciplinary research centres:
Our research
Research undertaken in the Department of Mathematical Sciences spans a wide range of key themes within science and technology. Our cutting-edge research uncovers both impactful and exciting outcomes that apply to many aspects of the modern world.
The mathematical sciences often form an 'unseen' part of our everyday lives, yet they underpin many aspects of the modern world. Mathematics is a key driver in advancing many areas within science and technology, making continued research in mathematics both impactful and exciting.
The researchers in our department collaborate with mathematicians, scientists and industry partners from around the globe to deliver top quality research. Our strengths were reflected in the latest Research Excellence Framework (REF) results (2021), where 100% of Mathematical Sciences research impact was rated 'world-leading' or 'internationally excellent'.
Analysis and PDEs
The research interests of the group include analysis of partial differential equations (PDEs), including hyperbolic equations and systems with multiplicities, microlocal, spectral and harmonic analysis, eigenvalue estimates for Dirac and Schrödinger type operators, inverse spectral transform method for integrable PDEs, applications to approximation theory, as well as other topics.
Dynamical Systems
This group studies a wide range of aspects of dynamical systems theory, such as Hamiltonian and dissipative dynamics, dynamical chaos in classical and quantum systems, dynamics of multi-scale systems, ergodic theory, random matrix theory, and bifurcation theory.
Geometry and Mathematical Physics
The research of the group covers a broad range of topics in geometry and related areas of mathematical physics, including the theory of both classical and quantum integrable systems. Another research focus is algebraic geometry, in particular, birational geometry and mirror symmetry.
Linear and Nonlinear Waves
The group’s interests are in wave motion in a variety of physical situations including geophysical fluid dynamics, water waves, solid mechanics, Bose-Einstein condensates, electromagnetism and acoustics. The group develop and apply exact, numerical, asymptotic and perturbation techniques to pursue research on linear and nonlinear waves with a focus on solitary waves and soliton theory, stochastic wave systems, wave generation, and diffraction and scattering by obstacles.
Mathematical Modelling
Members of the group apply a variety of techniques from applied mathematics to diverse problems in medicine, biology, fluid dynamics, materials and soft matter science. The biological systems studied range from intracellular processes to those at the scale of organisms and populations. The fluid flows studied range from environmental buoyancy-driven flows to technologically important micro- and nano-fluidic flows.
The modelling of materials involves the use of mathematical and computational techniques to solve a wide and varied class of problems. This includes nanoscale devices where the fate of individual atoms is important. It spans length scales and time scales that vary over many orders of magnitude and involves the solution of equations that range from continuum to quantum mechanical descriptions.
You can find further details on Mathematical Modelling.
Stochastic Analysis
Stochastic analysis is currently a very active and important basic research area in mathematics. Rooted in probability and measure theory, and beginning with the fundamental work of Wiener, Kolmogorov, Levy and Ito, stochastic analysis has intrinsic and deep connections. Furthermore, it has many applications in analysis and partial differential equations, geometry, dynamical systems, physics, geophysics, engineering, biology etc, in which many problems are modelled by stochastic differential equations or stochastic partial differential equations.
Stochastic analysis has become the basic mathematics for mathematical finance thanks to the pioneering idea of Black, Scholes and Merton. It has been a main research area in probability theory in recent years and the trend is still increasing. In our group, the research topics include:
- stochastic analysis, in particular interactions with analysis
- stochastic methods in (nonlinear) partial differential equations and mathematical physics
- stochastic dynamical systems
- stochastic differential equations
- stochastic partial differential equations
- infinite-dimensional analysis
- stochastic analysis on geometric spaces
- Markov processes and Dirichlet forms
- quantum stochastic analysis
- rough path
- Schramm Loewner evolution
- mathematics of finance.
Statistics
The Statistics group is involved in methodological research in contemporary issues in mathematical and computational statistics, as well as in making diverse applications to the natural, biological and social sciences, including engineering, medical imaging, astrophysics, materials science, ecology, testing theory, etc.
Your development
You will have at least two academic supervisors who will guide you in your research. You’ll also be provided with a desk, computer, photocopying facilities and can apply for funds for conference attendance.
A PhD programme will give you the opportunity to develop new and highly sought after skills which can set you up for a range of careers. It’s a chance to make a novel contribution to knowledge, to become a world expert in a particular field, and it can open a range of doors with different employers. You'll also enhance your interpersonal skills, such as networking and relationship building, which will be invaluable in your future career.
Our extensive training provision, supported by the Doctoral College, will also enhance your skills and experience as a researcher. You will enjoy a dynamic research atmosphere with regular workshops, international visitors and a wide range of research seminars to which you’ll be invited to make presentations.
Your future career
Graduates from the Department of Mathematical Sciences have gone on to pursue further research opportunities or academic careers. Others have taken up rewarding positions in diverse fields such as finance, software engineering, and data analysis.
Where you'll study
Our Department undertakes research in both pure and applied mathematics and is located in the refurbished Schofield Building. You will have access to spacious study areas, with the latest audio-visual equipment to support teaching and research.
Entry requirements
Our entry requirements are listed using standard UK undergraduate degree classifications i.e. first-class honours, upper second-class honours and lower second-class honours. To learn the equivalent for your country, please choose it from the drop-down below.
Entry requirements for United Kingdom
A minimum of a high 2:1 honours degree (or equivalent international qualification) in mathematics.
Afghanistan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Masters | 95% | 85% | 70% |
Albania
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diplomë e Nivelit të Pare (First Level (University) Diploma (from 2010) | 9.5 | 8.5 | 8 |
Algeria
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licence (4 year) / Diplome d'Inginieur d'Etat / Diplôme d'Etudes Supérieures | 16 | 14 | 12 |
Argentina
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciatura/ Licenciado (4 year) | 8.5 | 7.5 | 6.0 |
Armenia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalavri Kochum required but typically a Magistrosi Kochum | 90% or 3.9 | 80% or 3.5 | 70% or 3.0 |
Australia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Honours degree (AQF level 8) | First Class, 80% | Upper Second, 70%, H2A | Lower Second, 60%, H2B |
| Ordinary degree - AQF Level 7 pass (mark 46 or 50) | High Distinction (80% or 85%) | Distinction (75% or 80%) | Distinction (70% or 75%) |
Austria
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree / Diplomstudium / Fachhochschuldiplom (Diplom (FH)) | A (or 1.5) mit Auszeichnungbestanden | 60% / B / (or 2) | 60% / B / (or 2) |
Azerbaijan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalavr Diplomu/ Diplomu (Specialist Diploma) | 4.5 or 90% | 4 or 80% | 3.5 or 70% |
Bahamas
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree from University of the West Indies only | 1st (GPA 3.6) | 2:1 (GPA 3.0) | 2:2 (GPA 2.5) |
Bahrain
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.8 |
Bangladesh
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 year Bachelor of Science in Engineering (IEB and BAETE accredited courses only) | 1st (70%) / 3.5 | 2nd (60%) / 3.0 | 2nd (55%) / 2.75 |
| Masters (1-2 years) following a 3 or 4 year degree | 80% / 4.0 | 65% / 3.25 | 50% / 2.5 |
Belarus
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Specialist Diploma (5Yr) | 9 | 7 | 5 |
Belgium
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor degree/Licenciaat/Licencie | 80% or 17 | 70% or 14 | 60% or 12 |
Belize
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree from University of the West Indies only | 1st (GPA 3.6) | 2:1 (GPA 3.0) | 2:2 (GPA 2.5) |
Benin
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Maitrise | 18 | 15 or Bien | 12 or Assez Bien |
Bermuda
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree from University of the West Indies only | 1st (GPA 3.6) | 2:1 (GPA 3.0) | 2:2 (GPA 2.5) |
Bolivia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| A Licenciado, 4 years Private (public/private) | 85/78 | 75/66 | 67/55 |
Bosnia and Herzegovina
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma Visokog Obrazovanja / Diplomirani | 10 | 9 | 8 |
Botswana
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's degree | A or 80% | B or 70% | C or 60% |
Brazil
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Brazil - 4 yr Bacharel or Licenciado/Licenciatura or Título Profissional | 8.5 | 7.5 | 6.5 |
Brunei
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Brunei | First | Upper Second (60%/B/3.1) | Lower Second (50% or C or 2.5) |
Bulgaria
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 5 yr Diploma za Zavarsheno Visshe Obrazovanie (Diploma of Completed Higher Education) | 6 | 5 | 4 |
Burundi
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Masters or Diplôme d'Études Approfondies or Diplôme Ingénieur (professional title) | 18 | 15/20 (Bien) | 12.5/20 (Assez Bien) |
Cambodia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Masters | 80% or B+ or 3.5 | 70% or B or 3.0 | 60% or C+ or 2.5 |
Cameroon
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor degree or Diplome d'Etudes Superiures de Commerce or Diplome d'Ingenieur or Diplôme d'Ingénieur de Conception or a Maitrise, 4 year Licence or Master 1 (M1) | 1st / 3.6 or 15/Tres Bien | 2:1 / GPA 3.0 or 14 / Bien | 2:2 / GPA 2.5 or 12.5/ Assez Bien |
Canada
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0/Percentage | 3.7/85% | 3.3/75% | 2.7/68% |
| Out of 9 | 8 | 6 | 5 |
| Out of 12 | 10 | 8 | 6 |
Chile
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Grado de Licenciado / Título (Profesional) de [subject area] (4 years) | 6 | 5.5 | 5 |
China
Students are required to have a bachelor degree (4 years) for entry to a postgraduate programme. The University uses the Shanghai Academic Ranking of World Universities to identify the required final mark, as outlined on the table below:
| First class (70%) | Mid 2:1 (65%) | 2:1 (60%) | Mid 2:2 (55%) | 2:2 (50%) | |
|---|---|---|---|---|---|
| Shanghai Rank Top 250 | 83% | 79% | 75% | 73% | 70% |
| Shanghai Rank 251-500 | 88% | 84% | 80% | 78% | 75% |
| Shanghai Rank 501+ | 92% | 87% | 84% | 82% | 80% |
Affiliated colleges
The University will consider students from Affiliated Colleges in the following way:
Applicants from colleges affiliated to universities in the top 250 Shanghai rankings will be considered if they have achieved or are likely to achieve final marks of 75%-84%.
Applicants from colleges affiliated to universities which are 251-500 in the Shanghai rankings will be considered if they have achieved or are likely to achieve final marks of 80%-87%.
Applicants from colleges affiliated to universities which are above 500 in the Shanghai rankings will be considered as follows:
- School of Business and Economics: not considered
- All other programmes if they have achieved or are likely to achieve final marks of 80%-87%.
Universities given special consideration
Applicants from a small number of Chinese universities that specialise in business, management, finance or creative arts will be given special consideration by the University. The full list of these universities and the Shanghai band under which they will be considered can be found below:
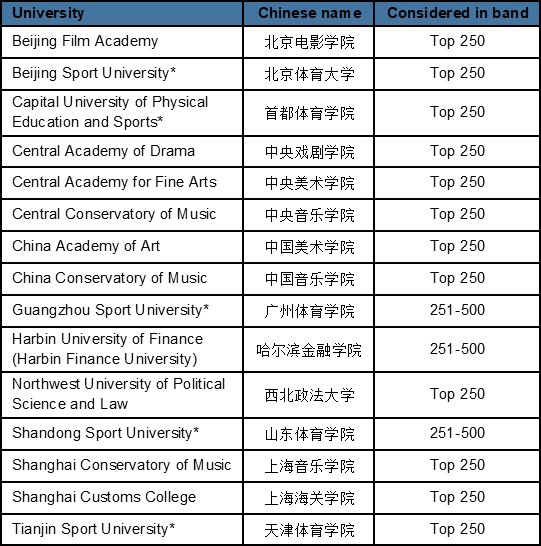
*Special consideration for programmes in School of Sport, Exercise and Health Sciences and Institute for Sport Business only.
Colombia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciado / Título de [subject area] | 4.5 | 3.75 | 3.2 |
Costa Rica
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciado | 9 | 8 or 80 | 7 or 75 |
Croatia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Baccalaureus / Prvostupnik | 4.5 | 3.8 | 3.0 |
Cuba
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4-year Titulo de Licenciado / Licenciatura | 5 | 4 | 3 |
Cyprus
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Cyprus | 8.5 | 7.0 | 6.5 |
Czech Republic
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalár (after 2001) 6 yr integrated Magistr | 1 | 1.5 | 2 |
Denmark
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 5 year Candidatus/Candidata Magisterii or Bachelor degree (7 point scale) | 12 | 10 | 7 |
Dominican Republic
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 year Licenciado or Título de [subject area] | 3.8 | Magna Cum Laude or 3.5 or 85% | Cum Laude or 3.2 or 82% |
Ecuador
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Título de Licenciado / Título de [subject area] | 8.5 / 85% | 8 / 80% | 7 / 70% |
Egypt
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Egypt | 3.5 | 3.2 | 2.8 |
| Universities only | BA 90%, BSc 85% | BA 80%, BSc 75% | BA 65%, BSc 65% |
El Salvador
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 5 year Licenciado, Título de Ingeniero/Arquitecto | 8.5, 85% | 7.5, 75% or Muy Bueno | 6.5, 65% or Bueno |
Estonia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalaureusekraad or Magister or Magistrikraad | 5 or 91% or A | 4 or 81% or B | 3 or 71% or C |
Ethiopia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Masters (up to 2025) | A / GPA 4.0 | A / GPA 3.5 | B / GPA 2.8 |
| 4-year Bachelor degree with thesis (from 2024) | A / GPA 4.0 | A / GPA 3.5 | B / GPA 2.8 |
| 5-year Bachelor degree (from 2025) | A / GPA 4.0 | A / GPA 3.5 | B / GPA 2.8 |
Finland
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Kandidaattii/Kandidat or the Maisteri/Magister | 3 (out of 3) or 4.5 (out of 5) | 2 (out of 3) or 3 (out of 5) | 1 (out of 3) or 2.5 (out of 5) |
France
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licence (3 years)/ Maitrise/ Diplôme d'Ingénieur | 14 | 13 | 11 |
Georgia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4-year degree (% = new system) | 5 (95%) | 4.0 (85%) | 3.5 (75%) |
Germany
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| German Bachelor/ Diplom, Magister Artium / Zeugnis über den Zweiten Abschnitt der Ärztlichen Prüfung | 1.5 | 2.5 | 3.0 |
Ghana
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Ghana | First | Upper second/60% | Lower second/50% |
Greece
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Universities | 8.5 | 7.0 | 6 |
| TEI and non-University Institutions | 8.5 | 7 | 6.5 |
Grenada
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree from University of West Indies - classification | 1st, 70% (GPA 3.6) | 2:1, 60% (GPA 3.00) | 2:2, 50% (GPA 2.5) |
| Degree from University of West Indies - grade / percentage | A | B / 75% | C / 55% |
| Degree from University of West Indies - GPA | 3.6 | 3.0 | 2.0 |
Guatemala
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Liceniado / Titulo de (subject area) - 4 years | 90% (public university) / 95% (private university) | 80% (public university) / 85% (private university) | 60% (public university) / 70% (private university) |
Guyana
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's | GPA 4 | GPA 3.5 | 3.0 |
Honduras
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Título de Licenciado / Grado Académico de Licenciatura (4 year degree) - GPA out of 5 | GPA 5 or 90% | GPA 4 or 80% | GPA 3.5 or 70% |
Hong Kong
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 1st or 3.5/4 | 2:1or 3/4 | 2:2 or 2.5/4 | 2.5 |
Hungary
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Alapfokozt or Egyetemi Oklevel / Bachelor | 4.5 | 3.5 | 3 |
Iceland
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Baccalaurreatus degree or Kandidatsprof/Candidatus Mag | 8.5 | 7.5 | 6.5 |
India
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Institutions listed on the National Institutional Ranking Framework | 65% (First) | 60% (First) | 55% (Upper second) |
| All other Indian institutions | 70% (First with distinction) | 65% (First) | 60% (First) |
Indonesia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Sarjana I (S1) from accredited Universities | 3.3 | 3.0 | 2.8 |
Iran
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Iran | 17 | 15 | 13 |
Iraq
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Iraq | 80% | 75% | 70% |
Ireland
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Republic of Ireland | First (70%) | Upper second (60%) | Lower second (50%) |
Israel
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 3 yr Bachelor Degree | 90% | 80% | 70% |
Italy
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma di Laurea | 109/110 | 100/110 | 90/110 |
Ivory Coast
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diplome d'Etude Approfondies, Diplome d'Etude Superieures or Diplome d'Etude Superieures | 16 | 14 (Bien) | 12 (Assez Bien) |
Jamaica
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| For degrees studied at The University of West Indies or degrees accredited by UCJ and CCCJ | 1st (GPA 3.6) | 2:1 (GPA 3.0) or B | 2:2, 50% (GPA 2.5) |
Japan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Gakushi – GPA 4.0 scale | 85% or A or 3.5 | 80% or B or 3.0 | 70% or C or 2.0 |
Jordan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3 or 3.5/5 or 75% | 2.5 (or 3.0/5) / 63% |
Kazakhstan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 5.0/percentage scale | 4.5 or 90% | 4 or 85% | 3.5 or 80% |
| GPA 4.33 scale | 3.9 | 3.7 | 3.2 |
| GPA 4.0 scale | 3.7 | 3.4 | 3 |
Kenya
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Kenya | First / 70% / A | Upper second / 60% / B | Lower second / 50% / C |
Kosovo
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Kosovo | 10 | 9 | 8 |
Kuwait
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.6 | 3.0 | 2.6 |
Latvia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Latvia | 9 | 7 | 6 |
Lebanon
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| American | 90% (3.5) | 80% (3.2) | 70% (2.8) |
| French | 18 | 15 | 12 |
Liberia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's | 4.0 or 90% | 3.5 or 85% | 3 or 80% |
Libya
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| BSc Engineering, Architecture, Medicine | 85 (3.6) | 75 (3.0) | 65 (2.5) |
| Other bachelor's degree from a university | 90 (4.0) | 85% (3.6) | 75% (3.0) |
Lithuania
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Lithuania | 9 | 8 | 7 |
Luxembourg
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Luxembourg | 18 (excellent) | 16 (tres Bien) | 14 (bien) |
Macau
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Macau | 1st or GPA 3.7 | 2:1 or GPA 3.0 | 2:2 or GPA 2.5 |
Macedonia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Magistar Дипломиран / Баццалауреус / Баццалауреа (Bachelor degree) | 10 | 9 | 8 |
Malawi
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's only | MSc 75% | MSc 70% | MSc 65% |
Malaysia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Classification | First Class | 2.1 | GPA 2.5 |
| GPA 4.0 scale | 3.5 | 3.0 | 2.8 |
Malta
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Malta | 1st (80%) | 2:1 (70%) | 2:2 (55%) |
Mauritius
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Mauritius | 1st or 70% | 2:1 or 60% | 2:2 or 50% |
Mexico
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciatura / Licenciado/ Título (Profesional) de [subject area] | 8.5 | 8 | 7 |
Moldova
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma de Licenţă (Diploma of Licentiate) | 9 | 8 | 7 |
Mongolia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Диплом Специалиста (Specialist Diploma) | 90% or 3.5 | 80% or GPA 3.2 | 70% or GPA 3.0 |
Montenegro
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma of Completed Undergraduate Studies or Diploma of Professional Undergraduate Studies | 10 (or 5.0) | 9 (or 4.5) | 8 (or 4.0) |
Morocco
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diplôme d'Ingénieur d'État, Diplôme d'Écoles Nationales de Commerce et de Gestion, Licence / Licence d'Études Fondamentales / Licence Professionnelle | 16 | 14 | 12 |
Mozambique
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Mestrado/ Grau de Mastre | 16 | 14 | 12 |
Myanmar (Burma)
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 2 year Master's degree | 5 or 85% | 5 or 75% | 4.5 or 65% |
Namibia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4-year Bachelor Honours (post 2008) or Masters | 80% or A | 70% or B | 60% or C |
Nepal
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's (after 3 year bachelor degree) | 80% or 3.7 GPA | 65% or 3.3 GPA | 60% or 3.0 GPA |
Netherlands
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Netherlands | 8 | 7 | 6 |
New Zealand
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Year Honours degree (480 credits) - Level 8 | First (7.0) | Upper Second (6.0) | Lower Second (4.0) |
| 3 Year degree (360 credits) - Level 7 | A+ (9.0) | A- (7.0) | B+ (6.0) |
Nicaragua
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciatura (4 year) | 90% | 80% | 70% |
Nigeria
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 7 point Scale | 6 | 5 | 3.0 (on 5 point scale) |
| 5 point scale | 4.5 | 3.8 | 3.5 |
| 4 point scale | 3.5 | 3 | 2.5 |
Norway
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Norway | A / 1.8 | B / 2.3 | C / 3.0 |
Oman
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.5 |
Pakistan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Year degree only (the higher of the 2 options) | A- or GPA 3.7 | B or GPA 3.0 | C+ or GPA 2.6 |
| 2 or 3 year Bachelor plus Masters | 1st (60%) plus GPA 3.7 | 2nd (55%) plus GPA 3.0 | 2nd (50%) plus GPA 2.6 |
Palestine
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor (4-years) | (85%) 3.5 | (80%) 3.0 | (70%) 2.5 |
Panama
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Year Licenciado / Título de [subject area] | 91 (A) | 81 (B) | 71 (C) |
Papua New Guinea
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor (Honours) Degree | 1st | 2:1 | 2:2 |
Paraguay
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Year Título de Licenciado / Título de [subject area] | 4.5 (85%) | 4 (80%) | 3.5 (75%) |
Peru
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Year Título de Licenciado / Título de [subject area] | 14 | 13 | 12 |
Philippines
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Degree from prestigious state universities or Centres of Excellence (COE) | Summa Cum Laude 4.0 / 96% / 1.0 | Magna cum Laude 3.5 / 92% / 1.5 | Cum Laude 3.0 / 87%/ 2.0 |
Poland
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor Degree (post 2003) Magister (pre- 2003) | 5 | 4.5 | 4 |
Portugal
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma de Estudos Superiores Especializados (DESE) or Licenciado | 18 | 16 | 14 |
Qatar
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.8 |
Romania
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diploma de Licenta/ Diploma de Inginer | 9 | 8 | 7 |
Russia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalavr/Specialist Diploma/Magistr | 4.5 | 4.0 | 3.5 |
Rwanda
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 year bachelor (Hons) degree (480 credits) | 1st, 16/20 (80%) | 2:1,14/20 (70%) | 2:2, 12/20 (60%) |
Saudi Arabia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.8 |
| GPA 5.0 scale | 4.5 | 3.75 | 3.5 |
Senegal
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Maitrise, Diplome d'Etude Approfondies, Diplome d'Etude Superieures or Diplome d'Etude Superieures Specialisees | 16/20 or Tres Bien | 14/20 or Bien | 12/20 or Assez Bien |
Serbia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Diplomirani/ Bachelor's degree | 9 | 8 | 7 |
Sierra Leone
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Honours degree or masters | 1st (70%) | 2:1 (60% or B) | 2:2 (50% or C) |
Singapore
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor (Hons) | First | Upper second | Lower second |
| GPA 4.0 scale | 3.7 | 3.0 | 2.7 |
| GPA 5.0 scale | 4.5 | 3.5 | 3.0 |
Slovakia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bakalár (from 2005) Magister / Inzinier | 1.5 or B | 2.0 or C | 2.5 or C/high D |
Slovenia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| University Diplom | 9 | 8 | 7 |
South Africa
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor (Honours) or B Tech after 4 yrs study | 1st or 75% | 2:1 or 70% | 2:2 or 60% |
South Korea
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA out of 4.5 | 4.0 / A | 3.5 / B | 3.0 / C+ |
| GPA out of 4.3 | 4.0 / A | 3.0 / B | 2.7 / C+ |
Spain
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciado / Título de Ingeniero / Título de Arquitecto | 8.5 | 7 | 6.5 |
| UCM grading | 3.0 | 2.0 | 1.5 |
Sri Lanka
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 year Professional degree or Bachelor Special or Honours degree | 90%, GPA 3.70 | 80%, GPA 3.30 | 70%, GPA 3.0 |
Sudan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 year degree | 1st, 70%, B+ | 2:1, 66% | mid 2:2, 60%, B |
Sweden
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Kandidatexamen or Magisterexamen | Overall grade of VG with a minimum of 120 credits at VG | B or Overall grade of VG with a minimum of 90 credits at VG | C or Overall grade of G with a minimum of 90 credits at G |
Switzerland
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Bachelor Degree, Diplom or Lizentiat (10/6/5) | 10 / 5.5 / 1 | 8 / 5 / 2 | 6 / 4 / 3 |
Syria
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| State universities 4 years of study | 80% | 70% | 60% |
| Private universities 4 years of study | 90% | 80% | 70% |
Taiwan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Category 1 (4 year degree) | 80% | 75% | 70% |
| Category 2 (4 year degree) | 85% | 80% | 75% |
Tajikistan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Диплом специалиста - Specialist Diploma | 5 | 4.5 | 4 |
Tanzania
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Tanzania | 1st | 2:1 | 2:2 |
Thailand
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.8 |
Trinidad and Tobago
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| For degrees studied at The University of West Indies or degrees accredited by ACTT | 1st or GPA 3.6 | 2:1 or GPA 3.0 | 2:2 or GPA 2.5 |
Tunisia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licence, Maîtrise, Diplôme National d'Ingénieu | 16 (tres bien) | 14 (bien) | 11 (assez bien) |
Turkey
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Lisans Diplomasi or a Műhendis Diplomasi | 3.5 | 3 | 2.5 |
Turkmenistan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 4 Yr Bakalavr, Specialist Diploma or Magistr | 5 | 4.5 | 4 |
Uganda
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Uganda | 1st or 4.4 | 2:1 or 3.8 | 2:2 or 3.0 |
Ukraine
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Dyplom Magistra or a Bachelors degree (11 / 5) | 4.5 | 4.0 | 3.5 |
United Arab Emirates
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.0 | 2.6 |
United States of America
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| GPA 4.0 scale | 3.5 | 3.2 | 2.8 |
Uruguay
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciado (4 year) | 9 | 8 | 7 |
Uzbekistan
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Majistr Diplomi / Diplomi (Specialist Diploma) | 90% or GPA 4.5 | 80% or GPA 4.0 | 70% or GPA 3.5 |
Venezuela
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Licenciado/Professional title. (4 year) | 18/20 or 8/9 | 16/20 or 7/9 | 14/20 or 6/9 |
Vietnam
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 10-point scale | 8.0 | 7.0 | 6.0 |
| 4-point scale | 3.5 | 3.0 | 2.8 |
Zambia
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| Master's | A or 4.0 or 80% | B+, 3.5 or 70% | B or 3.0 or 60% |
Zimbabwe
| First-class honours (70%) | Upper second-class honours (60%) | Lower second-class honours (50%) | |
|---|---|---|---|
| 3/4 year degree | 1st or 75% | 2:1 or 65% | 2:2 or 60% |
English language requirements
Applicants must meet the minimum English language requirements. Further details are available on the International website.
Fees and funding
Tuition fees for 2024-25 entry
UK fee
£4,786 Full-time degree per annum
International fee
£21,500 Full-time degree per annum
Tuition fees for 2025-26 entry
UK fee
£5,006 Full-time degree per annum
International fee
£22,360 Full-time degree per annum
Fees for the 2024-25 academic year apply to projects starting in October 2024, January 2025, April 2025 and July 2025. Fees for the 2025-26 academic year apply to projects starting in October 2025, January 2026, April 2026 and July 2026.
Tuition fees cover the cost of your teaching, assessment and operating University facilities such as the library, IT equipment and other support services. University fees and charges can be paid in advance and there are several methods of payment, including online payments and payment by instalment. Fees are reviewed annually and are likely to increase to take into account inflationary pressures.
How to apply
If you can't find an advertised project that fits your interests and experience, you can submit a research proposal to the Department of Mathematical Sciences to find a supervisor who will work with you on your project. You can view our list of academic staff on our website or you can email us for guidance.
Your research proposal should include the aims of your study, a brief literature review, an outline of the proposed research methods, and your preferred member of staff to supervise the project. Further information on preparing your proposal can be found on the dedicated webpage.
You are strongly recommended to contact us before applying to discuss your topic, availability and funding.